We want to calculate the following division:
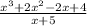
We start by dividing the leading term of the dividend by the leading term of the divisor:
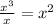
Then, we multiply this result by the divisor:
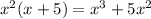
Subtract the dividend from the obtained result:
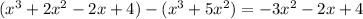
Then, we have:
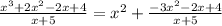
Since the second term can still be divided(the degree of the numerator polynomial is bigger than the degree of our divisor), we repeat the process:
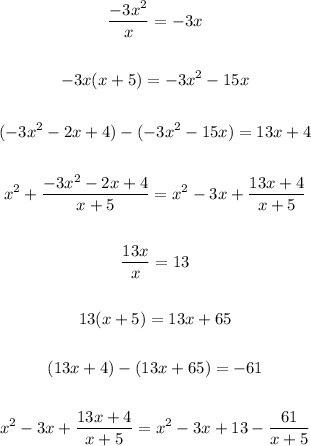
And this is our result:
