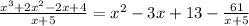Question

Using synthetic division find the quotient and remainder of x^3 + 2x^2-2x +4 divided by x+5

Answer 1

We want to calculate the following division:

`(x^3+2x^2-2x+4)/(x+5)`

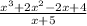
We start by dividing the leading term of the dividend by the leading term of the divisor:

`(x^3)/(x)=x^2`

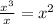
Then, we multiply this result by the divisor:

`x^2(x+5)=x^3+5x^2`

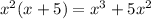
Subtract the dividend from the obtained result:

`(x^3+2x^2-2x+4)-(x^3+5x^2)=-3x^2-2x+4`

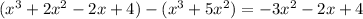
Then, we have:

`(x^(3)+2x^(2)-2x+4)/(x+5)=x^2+(-3x^2-2x+4)/(x+5)`

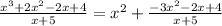
Since the second term can still be divided(the degree of the numerator polynomial is bigger than the degree of our divisor), we repeat the process:

`\begin{gathered} (-3x^2)/(x)=-3x \\ \\ -3x(x+5)=-3x^2-15x \\ \\ (-3x^2-2x+4)-(-3x^2-15x)=13x+4 \\ \\ x^2+(-3x^2-2x+4)/(x+5)=x^2-3x+(13x+4)/(x+5) \\ \\ (13x)/(x)=13 \\ \\ 13(x+5)=13x+65 \\ \\ (13x+4)-(13x+65)=-61 \\ \\ x^2-3x+(13x+4)/(x+5)=x^2-3x+13-(61)/(x+5) \end{gathered}`

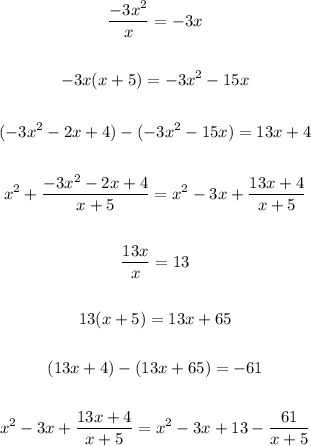
And this is our result:

`(x^(3)+2x^(2)-2x+4)/(x+5)=x^2-3x+13-(61)/(x+5)`