Question

Consider the logarithmic function f(x) = log10(x).

The value of f(50), rounded to nearest hundredth, is

Answer 1

Using the logarithmic rules:

`\log_b a = (\log a)/(\log b)`

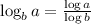
Given the logarithmic function:

`f(x) = \log_(10) x`

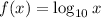
We have to find the value of f(50), rounded to nearest hundredth.

Substitute the value of x = 50 in [1] we have;

`f(50) = \log_(10) 50`

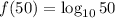
Apply the logarithmic rules:

`f(50) = (\log 50 )/(\log 10)`

Simplify:

`f(50) = (1.69897000434)/(1)`

⇒
`f(50)=1.69897000434`

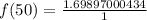
Therefore, the value of f(50), rounded to nearest hundredth, is 1.70

Answer 2

`log_(10) 50=1.70`