Question

For an angle θ with the point (15, −8) on its terminating side, what is the value of cosine?

Answer 1

cos x = adyacent side / hypothenuse

adyacent side = x = 15

hypothenuse = √(x^2 + y^2) = √[(15)^2 + (-8)^2] = 17

cos x = 15/17 ≈ 0.88

Answer 2

The value of cosθ is
`(15)/(17)`

Explanation:

It is given that an angle θ with the point (15, −8) on its terminating side.

Here x=adjacent side=15 units and y=opposite side =-8 units,

Using pythagoras theorem,

`\text{hypotenuse}^2=\text{base}^2+\text{opposite side}^2`

`\text{hypotenuse}^2=(15)^2+(-8)^2`

`\text{hypotenuse}^2=225+64=289`

`\text{hypotenuse}^2=17`

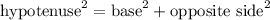
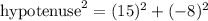
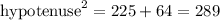
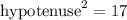
Cosine is defined as

`\cos \theta=(base)/(hypotenuse)`

`\cos \theta=(15)/(17)`

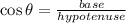
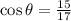
Therefore the value of cosθ is
`(15)/(17)`.