Answer: slope = 3
y - intercept = -2
Equation = y = 3x - 2
According to the graph, the points are (2, 4) and (0, -2)
Points: (2, 4) and (0, -2)
Firstly, we need to find the slope of the graph
Slope = rise / run
rise = y2 - y1
run = x2 - x1
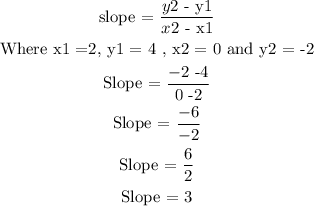
The standard form of slope intercept form of equation is given as y = mx + b
(y - y1) = m (x - x1)
where m = slope, and b = intercept
y1 = 4 and x1 = 2
(y - 4) = 3(x - 2)
Open the parentheses
y - 4 = 3x - 6
isolate y
y = 3x - 6 + 4
y = 3x - 2