Question

How does the graph of y=1/2(x+4)^2 compare to the graph of y=(x-1)^2-3

Answer 1

The graph of y = 1/2(x + 4)^2 is a shrink of y = (x - 1)^2 - 3
The vertex of the graph of y = 1/2(x + 4)^2 is 5 units to the left and 3 units up of the vertex of the graph of y = (x - 1)^2 - 3.

Answer 2

Vertical stretch and compression:

Given a function f(x) , a new function g(x) =a f(x), where a is the constant, is a vertical stretch or vertical compression of the function f(x).

• if 0<a<1 , then the graph will be compressed

• if a > 1 the graph will be stretched .

• if a<0, then there will be combination of a vertical stretch or compression with a vertical reflection.

In general if a function is shifted a units right and b units down we can summaries this as:

f(x) is shifted a units right and b units down
`\rightarrow` f(x-a) -b

Given the function:
`y = (1)/(2)(x+4)^2`

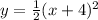
Now, replace y with
`2 y` results in a vertical stretch by a factor of 2.

⇒
`y = (x+4)^2`

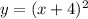
Then, by definition of above;

now, shift function
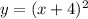`y = (x+4)^2` as 5 units right and 3 units down we have;

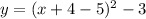`y = (x+4-5)^2 -3` or

`y = (x-1)^2 -3`

Therefore, the transformation from the graph
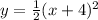`y = (1)/(2)(x+4)^2` is vertically stretch by a factor 2 and it is shift to 5 units right and 3 units down we have then,
`y = (x-1)^2 -3`

Also, you can see the graph shown below;