Answer:
B.
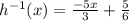
Explanation:
We have been given a function
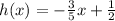 . We are asked to find the inverse function of our given function.
. We are asked to find the inverse function of our given function.
First of all, we replace h(x) by y as:
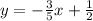
To find inverse of our given function we will interchange x and y variables and solve for y.
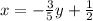
Upon subtracting 1/2 from both sides of equation, we will get:
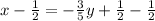
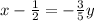
Let us have a common denominator.
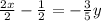

Multiplying both sides by
 ,
,
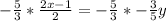
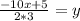
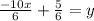
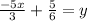
Replacing y by
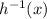 we will get,
we will get,
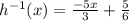
Therefore, the option B is the correct choice.
Therefore,