Answer:
g(x) =
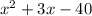 for real zero x= -8, x =5.
for real zero x= -8, x =5.
Explanation:
Given : real zeros x =-8 , x =5 .
To find : Function.
Solution : We have given that:
Factor theorem states that (x-r) is a factor of the polynomial function f(x) if and only if r is a root of the function f(x).
Since, we know that the root of the function i.e f(x) are -8 and 5 then the function has the following factor:
(x+8) = 0 and (x-5) =0
Zero product property states that if ab = 0 if and only if a =0 and b =0.
By zero product property,
(x+8)(x-5) = 0
Now, distribute each terms of the first polynomial to every term of the second polynomial we get;
x (x-5 ) +8(x-5)
 .
.
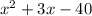 .
.
Therefore, g(x) =
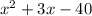 for real zero x= -8, x =5.
for real zero x= -8, x =5.