Question

P, Q, and R form the vertices of a triangle. QR = 7.8 RP = 15.7 and PQ = 11.6 Find the angle PRQ rounded to 1 DP

Answer 1

45.1°

Explanation:

A triangle is a polygon with three sides and three angles. The types of triangles are scalene triangle, equilateral triangle, right angled triangle and obtuse triangle.

Cosine rule states that given a triangle with sides a, b, c and their corresponding angles opposite to the sides as A, B, C. Then:

`a^2=b^2+c^2-2bc*cosA\\`

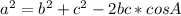
Given triangle PQR, let ∠PQR = x, to find angle PQR, we use cosine rule:

`PQ^2=QR^2+RP^2-2(QR)(RP)*cos(x)\\\\substituting:\\\\11.6^2=7.8^2+15.7^2-2(7.8)(15.7)cos(x)\\\\134.56=60.84+246.48-244.92cos(x)\\\\244.92cos(x)=60.84+246.48-134.56\\\\244.92cos(x)=172.76\\\\cos(x)=0.7054\\\\x=cos^(-1)(0.7054)\\\\x=45.1^o`

x = ∠PQR = 45.1°