Question

a concrete cube of side 0.50 m and uniform density 2.0 x 103 kg m–3 is lifted 3.0 m vertically by a crane. what is the change in potential energy of the cube

Answer 1

`U = 7357.5 J`

Step-by-step explanation:

Density of the cube is given as

`\rho = 2.0 * 10^3 kg/m^3`

volume of the cube is given as

`V = a^3`

here we have

a = 0.50 m

so we will have

`V = (0.50)^3`

`V = 0.125 m^3`

so we will have mass of the block given as

`mass = density * Volume[tex]</p><p>[tex]M = 0.125 * 2 * 10^3`

`M = 0.25 * 10^3`

now potential energy is given as

`U = mgh`

`U = 0.25 * 10^3 * 9.81* 3`

`U = 7357.5 J`

Answer 2

Change in potential energy = 7350 Joules

Step-by-step explanation:

It is given that,

Side of cube, a = 0.5 m

Density of cube,
`d=2* 10^3\ kg/m^3`

The cube is lifted vertically by a crane to a height of 3 m

We know that, density
`d=(m)/(V)`

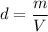
So, m = d × V (V = volume of cube = a³)

`m=2* 10^3\ kg/m^3* (0.5\ m)^3`

m = 250 kg

We have to find the change in potential energy of the cube. At ground level, the potential energy is equal to 0.

Potential energy at height h is given by :

`PE=mgh`

PE = 250 kg × 9.8 m/s² ×3 m

PE = 7350 Joules

So, change in potential energy of the cube is 7350 Joules.