For an equation of a parabola of the form: y = ax² + bx + c we can determine if the parabola opens upward or downward by analyzing the value of the first coefficient "a", if a is a negative number then the parabola opens downwards. We can get an equation of the mentioned form from f(x) = (x + 3)(x - 1) like this:
f(x) = (x + 3)(x - 1) = x² - x + 3x - 3 = x² + 2x - 3
As you can see, a equals 1, then the parabola opens upward
The x-intercepts of the function can be determined by calculating the values that make f(x) to be equal to 0, by replacing -3 and 1 for x into the function f(x) = (x + 3)(x - 1) you can easily prove that the x-intercepts are -3 and 1.
The coordinates of the vertex can be calculated by means of the following formula:

In this case, b equals 2 and a equals 1, by replacing these values into -b/2a, we get:
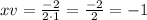
By replacing -1 for x into f(x), we get:
f(x) = ((-1) + 3)((-1) - 1) = (2)(-2) = - 4
Then, the coordinates of the vertex are (-1, -4)
The line of symmetry is a vertical line that passes through the vertex and has the form x = v, where v is the x-coordinate of the vertex. in this case, v equals -1, then the line of symmetry should be:
x = -1
The y-intercept of a parabola can be calculated by replacing 0 for x into the formula of f(x), then we get:
f(0) = (0 + 3)(0 - 1) = (3)(-1) = -3
Then, the y-intercept of the parabola equals -3