Question

Rafi measured the length of each scarf in the clothing store where he works. Length (centimeters) Number of scarves 108 3 155 2 249 3 252 2 271 2 273 7 280 1 X is the length of a randomly chosen scarf. What is the expected value of X? Write your answer as a decimal.

Answer 1

Let X be the length of a randomly chosen scarf. To find the expected value of X, we should first recall how to calculate the expected value.

When X can take only a discrete set of values, the expected value of X is calculated as follows

`E(X)\text{ = }\sum ^{}_{}xP(X=x)`

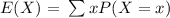
this formula means that we should multiply each possible value for x with the probability of having that value, and then adding all values together.

So, for example, one term of this sum in this case would be

`108\cdot P(X=108)`

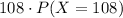
to calculate the term of the probability, we simply count how many scarfs we have of that length and divide it by the total amount of scarfs. So, we have 3 scarfs of length 108 and a total amount of 20 scarfs, so we have

`P(X=108)=(3)/(20)`

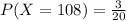
so, the first term would be

`108\cdot(3)/(20)=16.2`

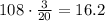
We can fill the following table using the principles explained above

x # of scarfs P(X=x) x*P(X=x)

108 3 0.15 16.2

155