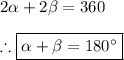Question

If PQRS is a rhombus, which statements must be true? Check all that apply.

Answer 1

The correct answers are:

PT = RT

PS is parallel to QR.

PR is perpendicular to QS.

PQR is supplementary to QPS.

Answer 2

These statements are true:


`\bold{First.} \ \overline{PS} \ is \ parallel \ to \ \overline{QR}`

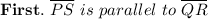
This is true because of the definition of a rhombus which states that opposite sides are parallel.


`Then \ \overline{PS} \ is \ opposite \ to \ \overline{QR}`


`\bold{Second.} \ \overline{PR} \ is \ perpendicular \ to \ \overline{QS}`

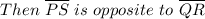
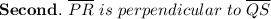
This is true because the diagonals of a rhombus bisect each other at right angles.


`\bold{Third.} \ \overline{PQ}=\overline{RS}`

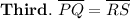
This is true because the four sides of a rhombus are all equals.


`\bold{Fourth.} \ \angle PQR \ is \ supplementary \ to \ \angle QPS`

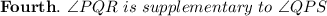
This is also true. Two angles are supplementary when they add up to 180 degrees. Angles in rhombus are equal two to two. Let's name:


`\angle PQR = \alpha \ and \ \angle QPS = \beta`

Then it is true that:


`\angle PQR=\angle PSR \ and \ \angle QPS=\angle QRS`

Besides, a rhombus is a quadrilateral and it is true that the interior angles of a quadrilateral add up to 360 degrees, thus:


`2\alpha+2\beta=360 \\ \\ \therefore \boxed{\alpha+\beta = 180^\circ}`