Question

Hello! I am in need of help! For the following problem I need to figure out (1.) IF THE LIMIT EXISTS, (2.) IF IT INDICATES THE EXISTENCE OF HORIZONTAL OR VERTICAL ASYMPTOTES, (3.) GIVE THE EQUATION OF SAID ASYMPTOTE, (4.) IF IT APPROACHES NEGATIVE OR POSITIVE INFINTY FROM THE LEFT AND RIGHT. I would HIGHLY appreciate any help! (This is a Calculus problem by the way)

Answer 1

Given the limit expression:

`\lim _(x\to\infty)(x^2+5x+6)/(2x^2+7x+3)`

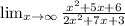
Factor both the numerator and denominator:

`\begin{gathered} x^2+5x+6=(x+2)(x+3) \\ 2x^2+7x+3=(2x+1)(x+3) \end{gathered}`

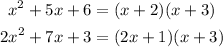
so,

`\lim _(x\to\infty)(x^2+5x+6)/(2x^2+7x+3)=\lim _(x\to\infty)((x+2)(x+3))/((2x+1)(x+3))=\lim _(x\rightarrow\infty)(x+2)/(2x+1)`

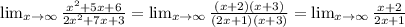
Now, divide the numerator and denominator by x:

`\lim _(x\rightarrow\infty)(x+2)/(2x+1)=\lim _(x\rightarrow\infty)(1+(2)/(x))/(2+(1)/(x))=(1+0)/(2+0)=(1)/(2)`

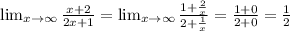
So, the answer is the value of the limit = 1/2

The answer indicates the horizontal asymptote

what would be the equation of said horizontal asymptote?

It will be: y = 1/2

The zeros of the denominator when 2x + 1 = 0

x = -1/2

At this point, the limit approaches to infinity from the right and the left

From the right, it will be positive infinity

From the left, it will be negative infinity

See the following figure: