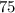Let
x-------> the number of shirts
y------> the number of jeans
we know that
 -------> equation
-------> equation

If she sold the shirts at
 profit and jeans at
profit and jeans at
 profit, her total profit was
profit, her total profit was
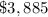
so
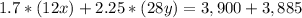
 -------> equation
-------> equation
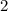
we have the following system of equations
 -------> equation
-------> equation

 -------> equation
-------> equation
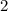
using a graph tool
see the attached figure
The solution of the system is the intersection both graphs
the solution is the point
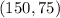
that means
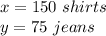
therefore
the answer is
the number of shirts is

the number of jeans is