Question

Bob has 20 feet of fencing to enclose a rectangular garden. If one side of the garden is x feet long, he wants the other side to be (10 – x) feet wide. What value of x will give the largest area, in square feet, for the garden?

Answer 1

Explanation:

Alright, lets get started.

The length of the rectangular garden is x

The width of the rectangular garden is (10-x)

So the area will be =
`length * width`

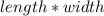
So the area will be =
`x*(10-x)= 10x-x^2`

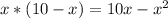
For this area to be maximum, the derivative of this area must be equal to zero.

`(d)/(dx)(10x-x^2) = 0`

`10-2x = 0`

`2x=10`

`x=5`

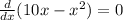
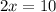
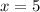
Hence the value of x will be for largest area. : Answer

Hope it will help :)

Answer 2

For the problem presented with the specific given values, the value of x that will give the largest area in square feet for the garden is 5. I am hoping that this answer has satisfied your query about this specific question.