Question

ABC is isosceles with AB=AC=8 units and BC=6 units. D and E are midpoints of AB and BC respectively. Calculate the length of DE?

Answer 1

We are given with an isosceles triangle with 8 units on two sides and 6 units on one side. The midpoint connecting two sides is called the mid-segment. The mid-segment is calculated using the law of cosines. Angle ABC is equal to 67.98 degrees. Using this angle, we compute the mid-segment using half of the other sides. The length is equal to 4 units. 

Answer 2

ABC is isosceles with AB=AC=8 units and BC=6 units.

ABC is a bigger triangle with AB = AC = 8 and BC = 6

Smaller triangle BDE is formed by connecting D and E that are midpoints of AB and BC respectively. D is the midpoint. AB =8 so AD = 4. Also BE = 4

Triangles ABC and BDE are similar triangles. so we make a proportion

`(DE)/(AC) =(BD)/(AB)=(BE)/(BC)`

`(DE)/(8) =(4)/(8)=(3)/(6)`

`(DE)/(8) =(4)/(8)`

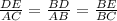
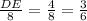
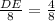
DE= 4

The length of DE = 4 units