Question

In the important industrial process for producing ammonia (the Haber Process), the overall reaction is:. N2(g) + 3H2(g) → 2NH3(g) + 100.4 kJ. A yield of NH3 of approximately 98% can be obtained at 200°C and 1,000 atmospheres of pressure. How many grams of N2 must react to form 1.7 grams of ammonia, NH3? A) 0.51 g. B)1.0 g. C) 1.4 g. D) 2.8 g

Answer 1

We are given with the equation that produces ammonia from the reaction of hydrogen gas and nitrogen gas. This is expressed in the balanced equation: N2+ 3H2 = 2NH3. We convert the given mass to moles of ammonia and multiply with the stoichiometric ratio of 1/2, further with the molar mass and the efficiency of the process. The N2 needed is 1.372 grams or C. 1.4 grams

Answer 2

Answer : The correct option is, (C) 1.4 g

Solution : Given,

Mass of ammonia = 1.7 g

Molar mass of ammonia = 17 g/mole

Molar mass of nitrogen = 28 g/mole

First we have to calculate the moles of ammonia gas.

`\text{ Moles of }NH_3=\frac{\text{ Mass of }NH_3}{\text{ Molar mass of }NH_3}=(1.7g)/(17g/mole)=0.1moles`

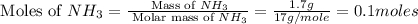
The given balanced reaction is,

`N_2(g)+3H_2(g)\rightarrow 2NH_3(g)`

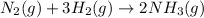
From the reaction, we conclude that

As, 2 moles of ammonia produced from 1 mole of nitrogen

So, 0.1 moles of ammonia produced from
`(1mole)/(2mole)* 0.1mole=0.05` moles of nitrogen

The moles of nitrogen = 0.05 moles

Now we have to calculate the mass of nitrogen.

`\text{ Mass of nitrogen}=\text{ Moles of nitrogen}* \text{ Molar mass of nitrogen}`

`\text{ Mass of nitrogen}=(0.05moles)* (28g/mole)=1.4g`

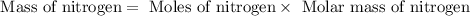
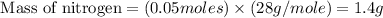
Therefore, the mass of nitrogen must be react is, 1.4 g.