Question

What are the possible number of positive real, negative real, and complex zeros of. f(x) = 4x3 + x2 + 10x - 14.

Answer 1

Answer: Positive roots = 1

Negative real root =0 or 2

complex roots=0 or 2

Explanation:

Given cubic polynomial f(x) =
`4x^3 + x^2 + 10x - 14`

By Descartes rules of signs

as this polynomial is already arranged in descending order and has only 1 sign change which means it has 1 positive real root.

Now change signs of coefficients of odd powered terms we get

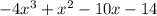`-4x^3 + x^2 - 10x - 14` then we have 2 sign changes which gives 2 or zero negative real roots .

For complex roots , we know that it is a cubic polynomial i.e. it has exactly 3 roots and complex roots always occur in pair, Therefore it will have zero or 2 complex roots.

Answer 2

1 sign change when x=1, there is 1 positve root

2 sign changes when x = -1. there are 2 possible negative roots

since complex roots come in 2s, there might be 0 negative roots, and 2 complex roots

close, but we cant say for sure that there are 0 or 2 negative roots; or 0 or 2 complex roots

Positive Real: 1

Negative Real: 0, or 2

Complex: 0, or 2