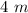Question

The top of a ladder is 10 meters from the ground when the ladder leans against the wall at an angle of 35.5° with respect to the ground. If the ladder is moved by x meters toward the wall, it makes an angle of 54.5° with the ground, and its top is 14 meters above the ground. What is x rounded to the nearest meter?

Answer 1

In the first triangle you can compute the base by taking the tan(35.5) and using the definition of tan.


In the second triangle you can compute the base by taking the tan(54.5) and using the definition of tan.

Subtract the two to get x.

x = 4.03

Answer 2

see the attached figure to better understand the problem

Step
`1`

in the triangle ABC

Find the distance AC

we know that

In the right triangle ABC

`tan(A)=BC/AC`

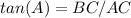
solve for AC

`AC=BC/tan(A)`

`BC=10\ m\\A=35.5\°`

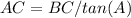
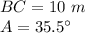
substitute the values

`AC=10/tan(35.5\°)`

`AC=14.02\ m`

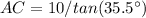
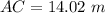
Step
`2`

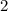
in the triangle DEF

Find the distance DF

we know that

In the right triangle DEF

`tan(D)=EF/DF`

solve for DF

`DF=EF/tan(D)`

`EF=14\ m\\D=54.5\°`

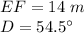
substitute the values

`DF=14/tan(54.5\°)`

`DF=9.99\ m`

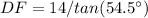
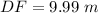
Step
`3`

Find the value of x

we know that

the value of x is the difference between AC and DF

`x=AC-DF`

`x=14.02-9.99=4.03\ m`

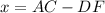
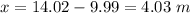
round to the nearest meter------->
`x=4\ m`

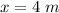
therefore

the answer is

The value of x is
`4\ m`