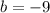Question

the axis of symmetry for the graph of the function f(x) =3/4 3x2 bx 4 is x =3/2 . what is the value of b?

Answer 1

Hello,
y=3x²+bx+3/4+4
= 3(x²+2b/6*x+b²/36)+19/4-b²/12
=3(x+b/6)²+19/4-b²/12
==>-b/6=3/2==>b=-9

Answer 2

The value of b is -9.

Explanation:

We are given a equation as:

`f(x)=(3)/(4)+3x^2+bx+4`

`f(x)=3x^2+bx+(19)/(4)`

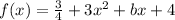
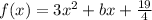
clearly the graph of this function will be a parabola.

for any quadratic equation of the type
`f(x)=ax^2+bx+c`

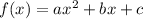
the equation of axis of symmetry is given by:

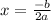`x=(-b)/(2a)` , here a=3 and b=b

also we are given axis of symmetry as
`x=(3)/(2)`

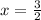
that means
`(-b)/(2*3)=(3)/(2)`

`b=-9`