Question

a projectile with an initial velocity of 48 feet per second is launched from a building 190 feet tall. the path of the projectile is modeled using the equation h(t) = –16t2 48t 190. approximately when will the projectile hit the ground? 1.5 seconds 3.2 seconds 5.3 seconds 6.2 seconds

Answer 1

I just graphed this equation, and it shows that the projectile will hit the ground at 5.3 seconds. I could be wrong but I'm going with the calculator is right I hope. I hope this helps you!

Answer 2

5.3 seconds

Explanation:

We have the motion equation as follows

`h(t) = -16t^(2)+ 48t +190`

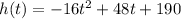
When the projectile touches the ground we have the height equal to 0

-16t^{2}+ 48t +190=0

we need to to solve this quadratic equation with:

`\frac{-b+\sqrt{b^(2)-4ac } }{2a}`

`\frac{-b-\sqrt{b^(2)-4ac } }{2a}`

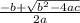
In this case A=-16, B=48, C=190

`\frac{-48+\sqrt{48^(2)-4*(-16)190 } }{2(-16)}`

`\frac{-48-\sqrt{48^(2)-4*(-16)190 } }{2(-16)}`

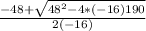
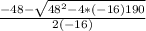
The results are -2.25 s and 5.3 s, since time is a positive variable the final answer is 5.3 seconds