Question

What is the axis of symmetry of the function f(x) = –(x 9)(x – 21)? the axis of symmetry is x =?

Answer 1

Hello,

y=-(x+9)(x-21)=-(x²-12x-189)=-(x²-2*6x+36)+189+36
=-(x-6)²+225

Vertex: (6,225)
Axis of symmetry: x=6

Answer 2

The axis of symmetry is x=6.

Explanation:

The given function is

`f(x)=-(x+9)(x-21)`

Using distributive property, we get

`f(x)=-(x^2-21x+9x-189)`

`f(x)=-x^2+12x+189` .... (1)

If a quadratic function is defined as

`y=ax^2+bx+c` .... (2)

then the axis of symmetry is defined as

`x=(-b)/(2a)`

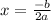
On comparing (1) and (2), we get

`a=-1,b=12,c=189`

The axis of symmetry of given function is

`x=(-12)/(2(-1))=6`

Therefore the axis of symmetry is x=6.