we have

This is a vertical parabola open upward
The axis of symmetry is equal to the x-coordinate of the vertex
The vertex is the point (h,k)
the equation of the axis of symmetry is
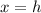
In this problem

so the x-coordinate of the vertex is

Convert the quadratic equation in vertex form
Group terms that contain the same variable, and move the constant to the opposite side of the equation

Factor the leading coefficient

Complete the square. Remember to balance the equation by adding the same constants to each side

Rewrite as perfect squares


remember that

so



substitute in the equation


therefore
the answer is
