Question

∠A and ∠B\angle B ∠B are supplementary angles. If m ∠A=(x−18)∘\angle A=(x-18)^{\circ} ∠A=(x−18) ∘ and m ∠B=(x−20)∘\angle B=(x-20)^{\circ} ∠B=(x−20) ∘ , then find the measure of ∠B\angle B ∠B.

Answer 1

∠B is 89°.

Explanation:

Answer 2

Given:

∠A and ∠B are supplementary angles.

m∠A=(x−18)° and m∠B=(x−20)°.

To find:

The measure of ∠B.

Solution:

Sum of supplementary angles is always 180 degrees.

∠A and ∠B are supplementary angles. So,

`m\angle A+m\angle B=180^\circ`

`(x-18)^\circ+(x-20)^\circ=180^\circ`

`(2x-38)^\circ=180^\circ`

`2x-38=180`

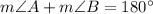
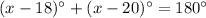
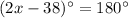
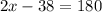
Now,

`2x=180+38`

`2x=218`

`x=(218)/(2)`

`x=109`

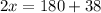
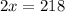
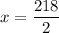
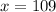
The measure of angle B is

`m\angle B=(x-20)^\circ`

`m\angle B=(109-20)^\circ`

`m\angle B=89^\circ`

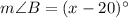
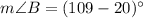
Therefore, the measure of ∠B is 89°.