Question

The angles in a triangle are represented by X, X+10, and x+50. What is the measure of the largest angle? 80°, 70°, 100°, 90°.​

Answer 1

Explanation:

x + x + 10 + x + 50 = 180°

• Sum of angles of ∆ is 180°

3x + 60 = 180°

3x = 120

x = 40

Angles are 40° , 50° , 90°

Here, The largest Angle is 90°

Answer 2

The largest angle in the triangle is the measure of 90° (answer choice D).

Explanation:

We are given that there are three angles in a triangle:

• x
• x + 10
• x + 50

We know that a triangle's interior angles will sum to be 180 degrees. With this information, we can create an equation in which we add all three values together and set the sum of them equal to 180 and solve for x.

Our equation will be combining the above three angles and setting them equal to 180.

To set up our equation, let's first add the three angle values together.

`\text{x + (x + 10) + (x + 50)}`

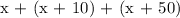
Then, we will set this value equal to 180 since the angles will add up to equal this amount.

`\text{x + (x + 10) + (x + 50) = 180}`

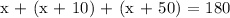
Now, we need to use simplifying techniques in order to be able to solve for x on both sides of the equation. Let's start by collecting our constants on the left side of the equation.

• Constants are values that do not have a variable attached to them and are just an integer or fraction.

We first can identify our constants.

• Constant #1: 10
• Constant #2: 50

These numbers are not our variable, or x, so therefore these are our constants. This is the easiest way to identify them.

The signs on both are addition, which means the integers are positive. Therefore, when combining them, we will add them together.

`\text{10 + 50 = 60}`

Now, we need to rewrite our equation. We no longer have a 10 or a 50, so we can do the following:

• Remove the 10 from the equation entirely.
• Replace the 50 with the new value: 60.

Therefore, our new equation will reflect these changes:

`\text{x + x + (x + 60) = 180}`

Now, we just need to combine our variables.

• First, let's count up how many we have: 3 x terms
• Take for example our x is a 4 instead. If we have 3 fours, we can simply multiply 4 by 3 to get our new value. The same concept applies to x-terms.
• Place a coefficient of 3 in front of the x in the (x + 60) term.
• This term becomes 3x + 60, we drop the parentheses, and we update our equation.

Our new rewritten equation will reflect the above changes.

`\text{3x + 60 = 180}`

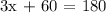
Now, we need to follow the steps to solve a two-step algebraic equation. These steps vary based on the equation, but we want to isolate our x term on either side of the equation (conventionally, we choose the left side) and our constant term on the opposing side.

In order to do this, we need to subtract the 60 from the left side of the equation to leave the x by itself. In order to do this, we also need to subtract 60 from 180. The rule in algebra states that the actions performed on one side of the equation must also be reflected on the opposing side of the equation.

• Just for reference, had the 60 been negative, we would have added it to the other side.

Therefore, by subtracting 60 from the left side, we also subtract 60 from the right side.

`\text{3x + 60 - 60 = 180 - 60}\\\\\text{3x = 120}`

Now that we have the x term isolated, we need to take note that we have a coefficient. This means that we need to isolate the x entirely. We are going to do this by dividing both sides of the equation by 3.

`(3x)/(3) = (120)/(3)\\\\\text{x = 40}`

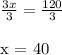
Now, we have solved for our x term. However, we are not done. We still need to find the measures of the angles, which is easily done by substituting our value for x (40) into the three expressions.

For our first expression:

`\text{x = 40}`

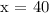
For our second expression:

`\text{40 + 10 = 50}`

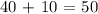
For our third expression:

`\text{40 + 50 = 90}`

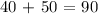
Now, to answer the final question, we need to find the measure of the largest angle.

Our three angle measures as determined above are:

• 40°
• 50°
• 90°

We can see that 90 is the largest number in the set, so our answer is 90°, or answer choice D.