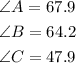Question

Apparently both angle A and angle C are not right please help

Answer 1

Given:

There are given that the triangle ABC.

Where,

`\begin{gathered} a=35, \\ b=34, \\ c=28. \end{gathered}`

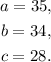
Step-by-step explanation:

To find the value of angles, we need to use the cosine rule:

So,

From the cosine rule:

`\begin{gathered} a^2=b^2+c^2-2bccosA \\ b^2=a^2+c^2-2accosB \end{gathered}`

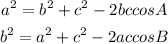
Now,

First, find the angle for A,

So,

From the formula to find the angle A:

`a^(2)=b^(2)+c^(2)-2bccosA`

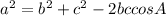
Then,

Put the value of a, b, and c into the above formula:

So,

`\begin{gathered} a^(2)=b^(2)+c^(2)-2bccosA \\ 35^2=34^2+28^2-2*34*28* cosA \\ 1225=1156+784-1904cosA \\ 1225=1940-1904cosA \end{gathered}`

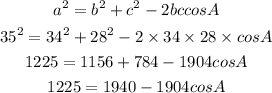
Then,

Subtract 1940 from both side of the equation:

`\begin{gathered} 1225=1940-1904cosA \\ 1225-1940=1940-1,904cosA-1940 \\ -715=-1904cosA \end{gathered}`

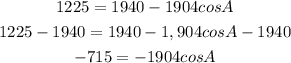
Then,

Divide by -1904 in both side of the above equation:

So,

`\begin{gathered} -715=-1904cosA \\ -(715)/(-1904)=-(1904)/(-1904)cosA \\ 0.3755=cosA \\ A=cos^(-1)0.3755 \\ A=67.9 \end{gathered}`

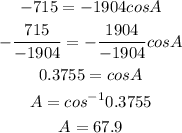
Now,

From the formula to find the angle for B:

`\begin{gathered} b^(2)=a^(2)+c^(2)-2accosB \\ 34^2=35^2+28^2-2*35*28* cosB \\ 1156=1225+784-1960cosB \\ 1156=2009-1960cosB \end{gathered}`

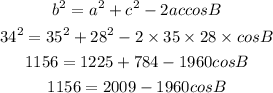
Then,

Subtract 2009 from both sides of the equation:

So,

`\begin{gathered} 1156=2009-1960cosB \\ 1156-2009=2009-1960cosB-2009 \\ -853=-1960cosB \\ cosB=(853)/(1960) \\ cosB=0.435 \\ B=cos^(-1)(0.435) \\ B=64.2^(\degree) \end{gathered}`

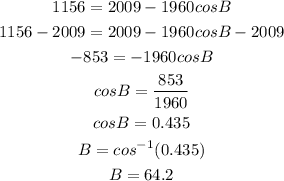
Now,

To find the angle C, we need to use the interior angle concept:

From the interior angle concept, addition of interior angle of any triangle is equal to 180 degrees.

Then,

`\angle A+\angle B+\angle C=180^(\degree)`

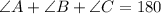
Then,

Put the value of angle A and angle B into the above formula:

So,

Final answer:

Hence, the value of angles A, B, and C are shown below:

`\begin{gathered} \angle A=67.9^(\degree) \\ \angle B=64.2^(\degree) \\ \angle C=47.9^(\degree) \end{gathered}`