Question

what is true about the function h(x) = x2 20x – 17? check all that apply. the vertex of h is (–10, –117). the vertex form of the function is h(x) = (x 20)2 – 17. the maximum value of the function is –17. to graph the function h, shift the graph of f(x) = x2 left 10 units and down 117 units. the axis of symmetry of function h is x = 20.

Answer 1

1 and 4

Explanation:

Answer 2

The correct options are 1 and 4.

Explanation:

The given function is

`h(x)=x^2+20x-17`

`h(x)=(x^2+20x)-17`

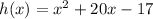
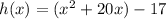
Add and subtract
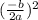`((-b)/(2a))^2` in the parentheses

`((-b)/(2a))^2=((-20)/(2(1)))^2=100`

`h(x)=(x^2+20+100-100)-17`

`h(x)=(x^2+20+100)-100-17`

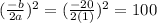
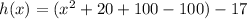
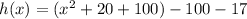
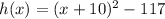`h(x)=(x+10)^2-117` ....(1)

The vertex form of the parabola is
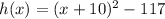`h(x)=(x+10)^2-117`. Option 2 is incorrect.

The general vertex form of a parabola is

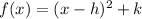`f(x)=(x-h)^2+k` ....(2)

Where, (h,k) is the vertex of the parabola.

On comparing (1) and (2) we get

`h=-10`

`k=-117`

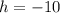
Therefore the vertex of the function is (-10,-117). Option 1 is correct.

It is upward parabola, so the minimum value of the function is -117. Option 3 is incorrect.

The vertex of the function f(x)=x² is (0,0) and the vertex of h(x) is (-10,-117).

It means the f(x) shifts left by 10 units and down 117 units. Option 4 is correct.

The axis of symmetry of the function is x=h.

So, the axis of symmetry is

`x=-10`

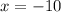
Therefore option is x=-10. Option 5 is incorrect.