Answer:
option (c) is correct.
The vertex form of given function
 is
is

Explanation:
Given :

We have to write h(x) in vertex form
For a given quadratic function
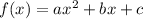 the vertex form can be written by completing square in such a way that we get, the equation in the form of
the vertex form can be written by completing square in such a way that we get, the equation in the form of
 , where (h,k) is the vertex.
, where (h,k) is the vertex.
Consider the given function

first writing in standard form , we get,

Using identity,
 , we have
, we have
x = a , and 2ab = 10x
Comparing , we get, b= 5
we need to add
 term
term
So add and subtract 25 in the given function , we get,

Simplify , we get,

Thus, the vertex form of given function
 is
is

option (c) is correct.