Answer:
option (2) is correct.
The vertex is (3 , -7)
Explanation:
Given: the function
 written in vertex form is
written in vertex form is

We have to write the vertex form of g(x).
For a given quadratic function
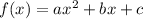 , we can rewrite it in vertex form
, we can rewrite it in vertex form
 , where (h , k) represents the vertex of the function f(x).
, where (h , k) represents the vertex of the function f(x).
For the given quadratic function
 written in vertex form is
written in vertex form is

On comparing , we get
h = 3 and k = -7
Thus, the vertex is (3 , -7)
Thus, option (2) is correct.