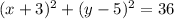Answer:
The general equation of the circle is given by:
 where r is the radius of the circle and (h, k) is the center of the circle.
where r is the radius of the circle and (h, k) is the center of the circle.
To shift any function upwards b units , then the center of the circle becomes;
(h, k+b)
As per the given statement:
equation of the circle is given by:
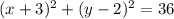
Center of this circle is: (-3, 2) and radius(r) = 6
to shift this equation of circle 3 units up then;
(h, k+3) = (-3, 2+3) = (-3, 5)
then;
the equation of circle 3 units upwards with radius = 6 units and center = (-3, 5) become:
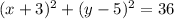
Therefore, the result of shifting a circle with equation
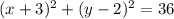 up 3 units is:
up 3 units is: