Answer:
The volume of the smaller sphere is 864 in³.
Explanation:
Let
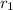 are
are
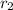 are the radius of the spheres,
are the radius of the spheres,
Thus, the surface area of the first sphere,
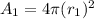
And, the surface area of the second sphere,

According to the question,

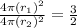
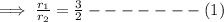
Now,
The volume of first sphere,
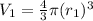
And, the volume of second sphere,
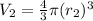
![\implies (V_1)/(V_2)=((4)/(3)\pi (r_1)^3)/((4)/(3)\pi (r_2)^3)</p><p>[tex]=((r_1)/(r_2))^3](https://img.qammunity.org/2017/formulas/mathematics/high-school/c6h8oo54fn10vfx5hnbmg6p7ry8xcak32w.png)
From equation (1),

Given,
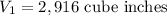

[tex]8\times 2,916=27V_2/tex]
[tex]23328=27V_2\implies V_2=864\text{ cube in}/tex]
Hence, the volume of the smaller sphere is 864 in³.