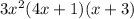Question

Which is the completely factored form of 12x4 + 39x3 + 9x2?

Answer 1

Answer: The completely factored form will be

`3x^2(4x+1)(x+3)`

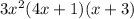
Explanation:

Since we have given that

`12x^4 + 39x^3 + 9x^2`

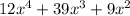
We need to find the factored form,

So, here we go:

1) Taking out the common factor i.e. 3x² :

`12x^4 + 39x^3 + 9x^2\\\\3x^2(4x^2+13x+3)`

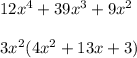
2) We get a quadratic equation , we will split the middle term:

`(4x^2+13x+3)\\\\4x^2+12x+x+3=0\\\\4x(x+3)+1(x+3)=0\\\\(4x+1)(x+3)=0`

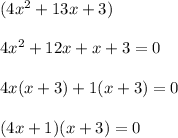
3) Now, combine the all of the factors:

`3x^2(4x+1)(x+3)`

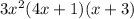
Hence, the completely factored form will be

`3x^2(4x+1)(x+3)`

Answer 2

Hello,

12x^4+39x^3+9x²=x²(12x²+39x+9)=x²(12x²+36x+3x+9)=x²(4x(3x+9)+(3x+9))
=x²(3x+9)(4x+1)
=3x²(x+3)(4x+1)