Question

for the simple harmonic motion d = 9cos (pi//2t), what is the maximum displacement from the equilibrium position?

Answer 1

y = A cos (B(x - C) + D

A gives the amplitude, which is the maximum displacement, so it's 9.

Answer 2

The maximum displacement from the equilibrium position is 9.

Explanation:

The given simple harmonic motion is:

`d=9cos((\pi)/(2)t)`

Differentiating above equation with respect to t, we get

`d'=-9sin((\pi)/(2)t)((\pi)/(2))`

⇒
`d'=-\frac{9{\pi}}{2}sin((\pi)/(2)t)`

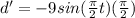
Again differentiating the above equation with respect to t, we have

`d''=-\frac{9({\pi})^(2)}{4}cos((\pi)/(2)t)<0`

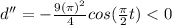
Now,
`d'=0`

⇒
`-\frac{9{\pi}}{2}sin((\pi)/(2)t)=0`

⇒
`sin((\pi)/(2)t)=0`

⇒
`(\pi)/(2)t=0`

⇒
`t=0`

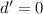
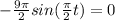
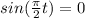
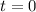
Substituting the value of t=0 in d, we get

⇒
`d=9cos((\pi)/(2)(0))`

⇒
`d=9cos(0)`

⇒
`d=9(1)`

⇒
`d=9`

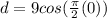
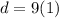
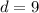
Therefore, the maximum displacement from the equilibrium position is d= 9.