Question

What are the zeros of the quadratic function f(x) = 6x2 + 12x – 7?

Answer 1

Use the quadratic formula
[-12 +/- square root (12^2- (4)(6)(-7))]/2(6)
[-12 +/- square root (312)]/12

-1+(1/6) square root (78)
and
-1-(1/6) square root (78)

Answer 2

A quadratic equation is of the form:
`ax^2+bx+c= 0` .....[1] where

a. b and c are coefficient and x is the variable.

The solutions of the equation are;

`x = (-b\pm√(b^2-4ac))/(2a)`

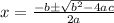
Given the function:
`f(x) = 6x^2+12x-7`

To find the zero of this function.

Set f(x) = 0

⇒
`6x^2+12x-7=0`

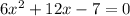
On comparing this with equation [1] we have;

a = 6, b = 12 and c = -7

then;

`x = (-12\pm√((12)^2-4(6)(-7)))/(2(6))`

`x = (-12\pm√(144+168))/(12)`

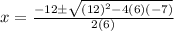
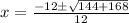
or

`x = (-12\pm√(312))/(12)`

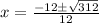
or

`x = (-12\pm 2√(78))/(12)`

`x = (-6\pm √(78))/(6)`

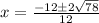
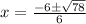
Therefore, the zeros of the quadratic function f(x) are;

`(-6+√(78))/(6)` and
`(-6-√(78))/(6)`