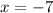Question

At which root does the graph of f(x) = (x + 4)^6(x + 7)^5 cross the x axis?

Answer 1

The Graph crosses at x -7

Explanation:

Answer 2

ANSWER

The graph of

`f(x) = {(x + 4)}^(6) {(x + 7)}^(5)`
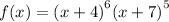
crosses the x-axis at

`x = - 7`


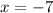
EXPLANATION



The nature of the multiplicity of a given polynomial function determines whether the graph crosses the x-axis at that intercept or not?





`f(x) = {(x + 4)}^(6) {(x + 7)}^(5)`

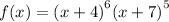
If the multiplicity of the factor is even as in

`{(x + 4)}^(6)`
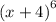
the graph touches but does not cross the x-axis at the intercept where

`x = - 4`
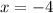
This means that the x-axis is a tangent to the function at this point.



However, if the multiplicity is odd, as in

`({x + 7})^(5)`
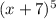
the graph crosses the x-axis at the intercept where

`x = - 7`