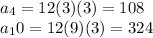Question

find the first, fourth, and tenth terms of the arithmetic sequence described by the given rule. a(n) = 12 (n–1)(3) a. 0, 9, 27 b. 12, 24, 42 c. 12, 21, 39 d. 3, 24, 27

Answer 1

No option suits this answer.

Explanation:

Given is an arithmetic sequence with general term formula in n as

`a_n = 12(n-1)+3`

We can find any general term by substituting for n

n =1

`a_1 = 12(1-1)(3)=0`

I term is 0

II term is got by substituting n =2

`a_2=12(2-1)3=36`

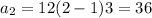
Hence common difference

`d=a_2-a_1\\d=36-0 =36`

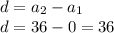
Hence the successive term would increase by 36

4th term

=
`a_4 =12(3)(3) =108\\a_10 = 12(9)(3) = 324`

Answer 2

First term a=0
Fourth term= 12(4-1)3
=12*9
=108

10th term=12(10-1)3
=12*9*3
= 324