Answer
c) carter
Explanation
Remember that A geometric sequence is a sequence where each term after the first is found by multiplying the previous term by a fixed number called the ratio. So to prove if a sequence is geometric, y we just need to verify that the ratio between any tow terms of the sequence is the same.
Now, to find the ratio of a geometric sequence, we use the formula:
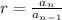
 is the ratio
is the ratio
 is the current term
is the current term
 is the previous term
is the previous term
The formula just mean that we can find the ratio by dividing the current term and the previous term.
Let's apply this to our sequences:
Angela -6,-9,-12,-15,...
Take -9 as the current term and -6 as the previous term, so
 and
and
 ; now let's find the ratio.
; now let's find the ratio.
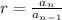

Lets check if the ratio hold for the next pair -9 and -12.
 and
and
 , so
, so
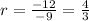
The ratio is not the same, so Angela's sequence is not a geometric one.
Bradley -2,-6, -12,-24,...
For -2 and -6
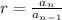
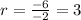
For -6 and -12
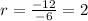
The ratio is not the same, so Bradley's sequence is not a geometric one.
Carter -1, -3, -9, -27,...
For -1 and -3
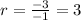
For -3 and -9
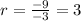
For -9 and -27
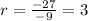
The ratio is always the same, so Carter's sequence is a geometric one.
Dominique -1, -3,-9, -81,...
For -1 and -3
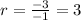
For -3 and -9
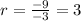
For -9 and -81
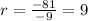
The ratio is not the same, so Dominique's sequence is not a geometric one.