Question

Find an equation of the line that satisfies the given conditions: t hrough ( 1/2

, −  2/3) ;   perpendicular to the line  6x − 12y = 1

Answer 1

Given:
equation of line l : 6x -12y =1
Converting the equation to slope-intercept form , we get,
-12y = 1 - 6x

y =
`(-6x+1)/(-12)`

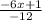
y = (1/2)x - (1/12)

Now, The when you find the equation of a perpendicuilar line, then the slope is the negative reciprocal of the slope of the given line. So,
y = -2x + b..........we didn't put anything for y-intercept because we don't know the y intercept of the perpendicular line yet.

Now, plugging the points from the question into the equation of perpendicular line, we get,
(-2/3) = -2*(1/2) + b
(-2/3) = -1 + b
(-2/3) + 1 = b
(1/3) = b

Now, plugging the value of b in the equation, we get,
y = -2x + (1/3).........this is your required equation

Answer 2

first make the equation to slope intercept
y=1/2-1/12
the slope of the perpendicular is equal to the negative inverse
m=-2
now substitute known variable in slope intercept form
-2/3=-2(1/2)+b
-2/3=-1+b
b=1/3
y=-2x+1/3
in standard
6x+3y=1