Question

Function g is a transformation of the parent function fx) = x2. The graph of g is a translation right 3 units and down 5 units of the graph off. Whatis the equation of function g written in the form y = ax + bx + c?

Answer 1

`f(x)=x^2`

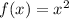
Since f(x) is translated 3 units right that means x will change to (x - 3)

Since f(x) is translated down 5 units that means f(x) is subtracted by 5

So:

`g(x)=(x-3)^2-5`

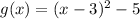
x changed to (x - 3) and f(x-3) changed to f(x-3) - 5

Since f(x) = x^2 so f(x - 3) = (x - 3)^2

Since f(x - 3) -5 = (x - 3)^2 - 5

So g(x) = (x - 3)^2 - 5

This is the vertex form

But the question asks for y = ax^2 + bx + c

So we must change it

g(x) = y

`y=(x-3)^2-5`

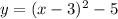
Solve the bracket

`(x-3)^2=(x-3)(x-3)=(x)(x)+(x)(-3)+(-3)(x)+(-3)(-3)`

Add like terms

`(x-3)^2=x^2-3x-3x+9=x^2-6x+9`
`\begin{gathered} y=x^2-6x+9-5 \\ y=x^2-6x+4 \end{gathered}`

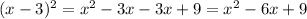
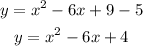
g(x) is y=x^2 - 6x + 4