Answer:
Part I: Let L = length of the section and let W = width of the section. The equation for the perimeter is P = 2(L + W). If the perimeter is 27 feet, solve for W. Show your work. (1 point)
27 = 2(L + W) 13.5 = (L + W) 35 = 3.5 x 10 3.5 + 10 = 13.5 W = 3.5
Part II: The equation for area is A = LW. Substitute the expression you found for W in Part I into the area equation. Then, if the area is equal to 35 square feet, write the equation in standard form with a, b, and c as whole numbers. (3 points)
L2 - 13.5L + 35 = 0
Part III: Use the quadratic formula, , to solve for L. Show your work. (2 points)
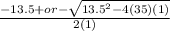
10 or 3.5
Part IV: Use the solution for L in Part III to find the corresponding values for W. Show your work. When you're done, state the dimensions of the section. (4 points)
L = 10 35 = LW 35 = 10 x 3.5 27 = 2(L + W) 27 = 2(10 + 3.5) 27 = 27
The length is 10 feet and the width is 3.5 feet.
Explanation:
Hope this helps