Question

using the graph calculator to graph the function f(x)=-√x. which list contain three points that lie on the graph of the function? (-9,3),(-4,2),(-1,1) (1,1),(4,2),(9,3) (-9,-3),(-4,-2),(-1,-1) (1,-1),(4,-2),(9,-3)

Answer 1

The list of points that lie on the graph of the function is:

(1,-1),(4,-2),(9,-3)

Explanation:

The square root function f(x) is given by:

`f(x)=-√(x)`

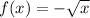
We know that the domain of the square root function is x ≥ 0

and when x ≥ 0

then √x ≥ 0

Hence,

`-√(x)\leq 0`

This means that the list of points must have x-coordinate as non-negative value and y-coordinate as non-positive value.

Now when x=1

we have:

`f(x)=-√(1)\\\\\\f(x)=-1`

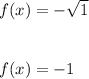
when x=4 we have:

`f(x)=-√(4)\\\\\\f(x)=-2`

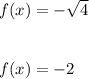
and when x=9 we have:

`f(x)=-√(9)\\\\\\f(x)=-3`

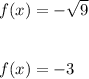
Hence, the points are:

(1,-1) , (4,-2) and (9,-3)

By plotting the graph of this function we may check the point.

Answer 2

x cannot be negative, so the first option and the third option are out.
when x = 1, f(x) = -1; when x = 4, f(x) = -2 and when x = 9, f(x) = -3. Hence the last option.