Question

Find the coordinates for the center for this circle.(x 3)² (y - 5)² = 25

Answer 1

(x - a)^2 + (y - b)^2 = c^2
above equation is the general equation for the circle. In that, a and b are center of the circle and c is the radius of the circle.

let's change the equation to general circle equation
(x - 3)^2 + (y - 5)^2 = 25
(x - 3)^2 + (y - 5)^2 = 5^2

center (3 , 5)
x = 3
y = 5

Answer 2

The equation
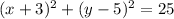`(x+3)^2+(y-5)^2=25` has coordinates for the center (-3, 5)

Explanation:

Given : Equation of circle as
`(x+3)^2+(y-5)^2=25`

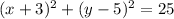
We have to fins the coordinates for the center for this circle.

The standard equation of circle with center (h,k) and radius r is given as

`(x-h)^2+(y-k)^2=r^2`

Consider the given equation
`(x+3)^2+(y-5)^2=25`

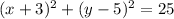
25 can be written as 5²

Rewrite it in standard form as ,

`(x-(3))^2+(y-5)^2=5^2`

where center is (-3, 5) and radius = 5

Thus, The equation
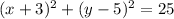`(x+3)^2+(y-5)^2=25` has center (-3, 5) and radius = 5