Question

solomon needs to justify the formula for the arc length of a sector. which expression best completes this argument? the circumference of a circle is given by the formula c=pi * d , where d is the diameter. because the diameter is twice the radius, c= 2 * pi * r. if equally sized central angles, each with a measure of n°, are drawn, the number of sectors that are formed will be equal to 360°/n° the arc length of each sector is the circumference divided by the number of sectors, or _____. therefore, the arc length of a sector of a circle with a central angle of n° is given by 2*pi*r*n/360 or pi*r*n/180 . a. 2*pi*r/270/n b. 2*pi*r/360/n c. 2*pi*r/180/n d. 2*pi*r/90/n

Answer 1

the numbers of sectors is 360/n

Then, the arc length is the circumference divided by 360/n which is the same that the circumference times n/360

So, the arc length is 2*pi*r/(360/n), which is the option b.

Answer 2

Answer: The answer is (b).
`(2\pi r)/((360^\circ)/(n^\circ)).`

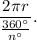
Step-by-step explanation: Let us consider a circle with centre "O" and radius OA=OB=r units. We know that the circumference of a circle is
`2\pi* radius~of~the~circle,` so the circumference of Circle 'C' is given by

`Circumference=2\pi r.`

Also, let us central angles of equal size of 'n°', the the number of sectors formed is given by

`no.~of~sectors=(360^\circ)/(n^\circ).`

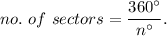
Now, the formula for arc length of a sector is given by

`arc~length~of~of~a~sector=(Circumference~of~the~circle)/(no.~of~equally~sized~sectors).`

∴
`arc~length~of~of~a~sector=(2\pi r)/((360^\circ)/(n^\circ)).`

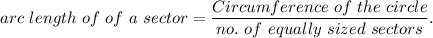
Thus, (b) is the correct option.