Question

Find s25 for 4 14 24 34

Answer 1

From the question, "s25" means the sum of the first 25 terms in the arithmetic sequence given. Given that the difference between each term is 10, the summation notation can be written as such:

24
∑ (4 + 10X)
n = 0

Such that, the sum of the first 25 terms is 3100..

Answer 2

The value of
`S_(25)` is 3100.

Explanation:

The given arithmetic sequence is

4, 14, 24, 34

First term of AP is 4 and common difference is

`d=a_2-a_1\Rightarrow 14-4=10`

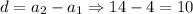
We need to find the value of
`S_(25)`. It means we have to find the sum of first 25 terms of the given AP.

The formula for sum of first n terms of an AP is

`S_n=(n)/(2)[2a+(n-1)d]`

where, n is number of terms, a is first term and d is common difference.

The sum of first 25 terms is

`S_(25)=(25)/(2)[2(4)+(25-1)(10)]`

`S_(25)=(25)/(2)[8+240]`

`S_(25)=(25)/(2)[248]`

`S_(25)=3100`

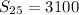
Therefore the value of
`S_(25)` is 3100.