Question

Hamza hits a golf ball into the air. It lands 200m away from him, having reached a height of 30 m. Assuming that the path of the ball is a quadratic relation, write its equation in vertex form. (Include a sketch.)

Answer 1

So,

We could draw the following situation:

As you can notice, we could take the zeros of the quadratic equation as:

`\begin{gathered} x=0 \\ x=200 \end{gathered}`

And, the y-coordinate of the vertex is 30.

Now, remember that a quadratic equation has the following general vertex form:

`y=a(x-h)^2+k`

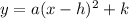
Where (h,k) are the coordinates of the vertex.

Now, given all the previous information, we need to find the value of a. The vertex of the parabola is (100,30) since it is symmetrical. And, when x=200, y=0. So,

`\begin{gathered} 0=a(200-100)^2+30 \\ 0=a(100)^2+30 \\ a(10000)=-30 \\ a=(-30)/(10000)=-(3)/(1000) \end{gathered}`

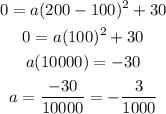
Thus, the equation of the parabola is:

`y=-(3)/(1000)(x-100)^2+30`

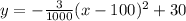
And, this is a sketch of it;