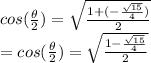Use the pythagorean identity to find cos Θ.
sin² Θ + cos² Θ = 1
(¼)² + cos² Θ = 1
cos Θ = ±(√15)/4
Now use the half angle identity
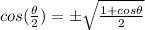
This is why you need to know the quadrant. If Θ is in Q1, then cos Θ is (√15)/4. If Θ is in Q2, then cos Θ = -(√15)/4.
Also, since Θ is in either Q1 or Q2, Θ/2 must be in Q1, and cos (Θ/2) is positive
For Θ in Q1:
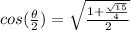
For Θ in Q2: