Question

Express the complex number 6 in complex trigonometric form.

Answer 1

Hello,

6=6*(cos 0 +i *sin 0)

Answer 2

6(cos 0° + sin 0° . i)

Explanation:

The trigonometric form formula is a combination of the following formulas:

Binomic: a + bi

Polar: rα

Giving as a result the formula: r (cos α + sin α · i)

Where,

r = module

α = angle

In the given case, the complex number is 6, where

Binomic form: 6 + 0i

Where a = 6 and b = 0

We must calculate the module (r) and the angle (α).

`r=\sqrt{a^(2) +b^(2)} =\sqrt{6^(2) +0^(2)}=√(36)=6`

α =
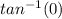`tan^(-1)(0)` = 0°

Since r=6 and α=0°, then the trigonometric form is

r(cos α + sin α · i) = 6(cos 0° + sin 0° . i)

Hope this helps!