Question

There is a population of 24,375 bacteria in a colony. If the number of bacteria doubles every 393 minutes, what will the population be 1,179 minutes from now?

Answer 1

We have the following informattion:

- Initial value of 24375

- It doubles every 393 minutes

- We want the population after 1179 minutes.

In an exponential equation, we have three mainparts:

`y=Ab^n`

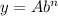
A is the initial value, always, so we have a directly relation:

`A=24375`

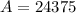
b is how much it changes in a given period. In this case, we have it double after the given period, so:

`b=2`

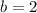
n is how many of this period have passed. 1 period is 393 minutes, so to calculate how many period of it we have, we get the total time (in minutes) and divide by the period we have. So, given t minutes passed, we have:

`n=(t)/(393)`

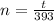
So, in the end, we have the equation:

`y=24375\cdot2^{(t)/(393)}`

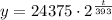
And now, we can just substitute any time in minutes to calculate the population after that time, in this case, we want t = 1179:

`t=24375\cdot2^{(1179)/(393)}=24375\cdot2^3=24375\cdot8=195000`

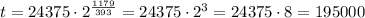
So, aftter that period, the population will be 195000.