We have the following informattion:
- Initial value of 24375
- It doubles every 393 minutes
- We want the population after 1179 minutes.
In an exponential equation, we have three mainparts:
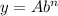
A is the initial value, always, so we have a directly relation:
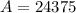
b is how much it changes in a given period. In this case, we have it double after the given period, so:
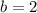
n is how many of this period have passed. 1 period is 393 minutes, so to calculate how many period of it we have, we get the total time (in minutes) and divide by the period we have. So, given t minutes passed, we have:
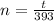
So, in the end, we have the equation:
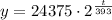
And now, we can just substitute any time in minutes to calculate the population after that time, in this case, we want t = 1179:
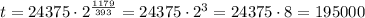
So, aftter that period, the population will be 195000.